Fluid's Enigma Unveiled: The Magnetic Forces of Stagnation, Static, and Dynamic Pressure
In the captivating world of fluid dynamics, forces relentlessly dance around us, orchestrating the intricacies of fluid behavior. Like master conductors, three key players stand out amidst the symphony of pressures, each with its unique allure and profound impact on the fluid realm. Welcome to the enthralling exploration of stagnation, static, and dynamic pressure – the foundational forces that shape the motion and equilibrium of fluids.
Imagine a fluid journey where motion meets resistance, where energy melds with inertia, and where the delicate balance of forces reveals mesmerizing phenomena. This journey begins with stagnation pressure, a notion that beckons us to the moment of fluid stillness, when fluid comes to rest within a flow field. Beyond mere cessation, it unravels a mystery: the confluence of static pressure, the steadfast guardian of fluid at rest, and dynamic pressure, the untamed surge born from fluid motion. Together, they blend into the grand crescendo of stagnation pressure – the essence of total impact at the point of halting.
As we delve deeper into this fluid symposium, static pressure emerges as the stoic anchor, defying the turbulence of change. With quiet constancy, it embodies the pressure at rest or in constant motion, unyielding to the fluid's tumultuous affairs. Yet, within its seemingly tranquil demeanor lies the equilibrium that governs fluid equilibrium and upholds the foundations of fluid engineering.
Rising in stark contrast to static pressure, dynamic pressure storms onto the stage with its unwavering ardor. A kinetic force pulsating with the fluid's very velocity, it surges forth, manifesting its might in the ethereal realm of fluid motion. Fluids in motion come alive as dynamic pressure bestows upon them the very essence of life, empowering them to sculpt the world around them with their sheer energy.
Together, these three titans of fluid dynamics weave a tapestry of intrigue, captivating researchers, engineers, and visionaries alike. From propelling aerospace engineering to sculpting wind energy systems, their influence embraces the world with grace and purpose. In this quest for knowledge, we seek to unravel their secrets, explore their boundless applications, and embrace the wonder they inspire in us.
Join us on this exhilarating journey as we traverse the realms of fluid dynamics, exploring the essence of stagnation, static, and dynamic pressure - the triumphant ensemble that harmonizes the symphony of fluid forces. Embark with us, for within this compelling exploration lies the key to unlocking the very secrets of nature's fluid dance.
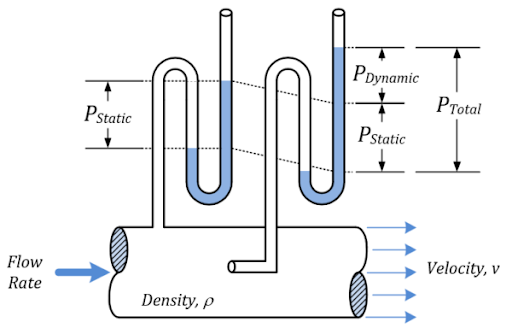
Fig 1. Different pressure scale
Stagnation pressure
Stagnation pressure, also known as total pressure or pitot pressure, is a concept used in fluid dynamics to describe the pressure of a fluid when it comes to a stop, or stagnates, in a flow field. It represents the sum of the static pressure and dynamic pressure of the fluid at a specific point in the flow.
In a moving fluid, such as air or water, there are two primary components of pressure:
- Static Pressure: This is the pressure exerted by the fluid due to its weight and molecular collisions. It is the pressure measured by a pressure gauge at rest relative to the fluid flow.
- Dynamic Pressure: This is the pressure related to the kinetic energy of the fluid particles in motion. It is a result of the fluid's velocity and is responsible for the pressure difference between moving and stationary objects in the flow.
When a fluid comes to a stop, either by impacting an object or by being brought to rest in a stagnation tube, the dynamic pressure is converted into static pressure. At this point, the total pressure or stagnation pressure is the sum of the static and dynamic pressures.
The concept of stagnation pressure is important in various engineering applications, such as in aerodynamics for measuring the velocity of a fluid flow using a Pitot tube or in the study of compressible flows in gas dynamics. It is denoted by the symbol "P0" and is often used as a reference point to calculate other flow parameters like the velocity of the fluid.
Find the best Pressure Sensor Products for your specific needs in our store.
Stagnation pressure usage
Stagnation pressure, also known as total pressure or pitot pressure, has several important uses in fluid mechanics and engineering applications. Here are some common usages of stagnation pressure:
- Aerodynamics: In aerodynamics, stagnation pressure is used to measure the total pressure of the fluid flow around an aircraft or any other object moving through a fluid. This measurement is crucial for determining the velocity of the fluid relative to the object, which is essential for calculating lift, drag, and other aerodynamic forces.
- Airspeed Indication: In aviation, a pitot tube is used to measure stagnation pressure, which, when combined with static pressure (measured by static ports on the aircraft), helps calculate the airspeed (indicated airspeed) of the aircraft. Indicated airspeed is a fundamental parameter for safe flight operations.
- Gas Dynamics: In gas dynamics and compressible flow analysis, stagnation pressure is a key parameter used to study the behavior of high-speed gas flows. It helps in understanding the impact of flow velocities on pressure and temperature changes, especially in supersonic flows.
- Wind Tunnel Testing: In wind tunnel experiments, stagnation pressure is measured to determine the total pressure at specific points in the flow field. This information helps researchers and engineers assess the aerodynamic performance of models and prototypes.
- HVAC Systems: In heating, ventilation, and air conditioning (HVAC) systems, stagnation pressure is used to measure the total pressure at various points in the ductwork. This data aids in optimizing the system's airflow and energy efficiency.
- Gas Turbine Engines: In gas turbine engines, stagnation pressure is measured at various stages of the engine to monitor its performance and efficiency.
- Rocket Propulsion: In rocket engines, stagnation pressure is a critical parameter for understanding the flow and combustion processes and optimizing thrust.
- Flow Calibration: In fluid flow measurement and calibration systems, stagnation pressure is used to calibrate flow meters and assess the accuracy of flow measurements.
- Atmospheric Studies: In meteorology and atmospheric science, stagnation pressure is used to study weather systems and atmospheric conditions.
In summary, stagnation pressure is a valuable parameter in fluid dynamics and engineering, providing essential information about fluid flow characteristics and the performance of various systems. Its applications range from aerodynamics and aerospace engineering to HVAC, gas dynamics, and atmospheric studies.
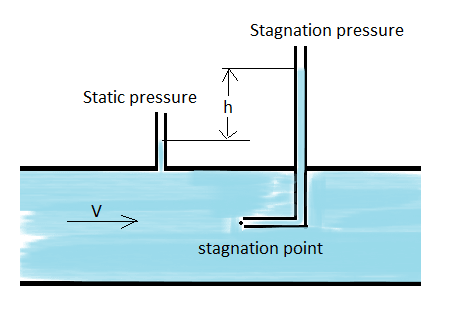
Fig 2. Static and stagnation pressure
Stagnation pressure formula
The stagnation pressure, denoted by P_0, is the total pressure of a fluid when it comes to rest (stagnates) in a flow field. It is the sum of the static pressure (P) and the dynamic pressure (q) of the fluid at a particular point in the flow. The formula to calculate stagnation pressure is as follows:
P0= P + q
P0= Stagnation pressure (total pressure) at a specific point in the flow (in pascals or any other pressure unit)
P = Static pressure at that point (in pascals or any other pressure unit),
q = Dynamic pressure at that point (in pascals or any other pressure unit).
To understand this formula better, let's briefly define the components:
Static Pressure (P): Static pressure is the pressure of the fluid when it is at rest or moving at a constant velocity in a particular direction. It is the pressure measured by a pressure gauge at rest relative to the fluid flow.
Dynamic Pressure (q): The dynamic pressure represents the kinetic energy per unit volume of a moving fluid. It is the pressure that arises due to the motion of the fluid. The formula for dynamic pressure is
q= ½ ρ. v^2
where:
ρ = Density of the fluid (in kg/m³ or any appropriate unit),
v = Velocity of the fluid at the point (in m/s or any appropriate unit).
By adding the dynamic pressure to the static pressure, we obtain the stagnation pressure, which represents the total pressure of the fluid when it comes to rest in the flow field.
It's important to note that the stagnation pressure can vary along the flow path, depending on changes in velocity and static pressure. In real-world scenarios, the calculation of stagnation pressure often requires experimental measurements or sophisticated computational fluid dynamics (CFD) simulations.
Static pressure
Static pressure is a fundamental concept in fluid mechanics and thermodynamics that refers to the pressure exerted by a fluid when it is at rest or moving at a constant velocity in a particular direction. It is the pressure measured in a fluid at a specific point in a flow field where the fluid is not accelerating.
In a fluid (liquid or gas), pressure arises due to the random motion and collisions of its molecules. When a fluid is at rest or moving at a constant velocity, the pressure at any given point in the fluid is equal in all directions. This isotropic pressure is referred to as static pressure.
Static pressure is a scalar quantity, meaning it has magnitude but no direction. It is typically measured using pressure gauges or sensors and is expressed in units of pressure, such as pascals (Pa), pounds per square inch (psi), or atmospheres (atm), depending on the unit system used.
In engineering and physics, static pressure plays a crucial role in various applications, including:
- Aerodynamics: In the study of airflows around objects like aircraft wings or cars, static pressure is essential for understanding lift and drag forces.
- HVAC (Heating, Ventilation, and Air Conditioning): Static pressure is used to design and optimize the airflow distribution in ventilation and air conditioning systems.
- Fluid flow in pipes: Static pressure is used to measure and analyze pressure drops and flow behavior in fluid transportation systems.
- Meteorology: Static pressure is measured to determine atmospheric pressure, which is essential for weather forecasting and climatology.
In summary, static pressure represents the pressure of a fluid when it is not accelerating or moving in any specific direction. It is an important parameter in the study of fluid dynamics and has practical applications in various engineering fields.
Static pressure formula
The static pressure formula depends on the context and the particular fluid flow situation. Here are the general formulas for static pressure in a few common scenarios:
- In a static fluid (fluid at rest):
In a fluid at rest, the static pressure is the same at all points within the fluid, and it depends only on the depth or height of the fluid column above the point being considered.
The formula for static pressure in a static fluid is
Pstatic =ρ⋅g⋅h
Pstatic = Static pressure (in pascals or any other pressure unit)
ρ = Density of the fluid (in kg/m³ or any appropriate unit)
g = Acceleration due to gravity (in m/s² or any appropriate unit)
h = Height or depth of the fluid column above the point (in meters or any appropriate unit)
- In a moving fluid (fluid in motion):
In a moving fluid, the static pressure varies based on the velocity and other flow characteristics. The total pressure (stagnation pressure) is the sum of the static pressure and the dynamic pressure, as explained in the previous response.
If you are dealing with a compressible fluid flow, such as air or gas, and you know the stagnation pressure and the dynamic pressure at a point, you can calculate the static pressure using the formula:
P_static = p_stagnation - ½ ρ. v^2
Pstatic= Static pressure (in pascals or any other pressure unit)
PStagnation = Stagnation pressure (in pascals or any other pressure unit)
ρ = Density of the fluid (in kg/m³ or any appropriate unit)
v = Velocity of the fluid at the point (in m/s or any appropriate unit)
It's important to note that these formulas represent simplified cases, and in real-world scenarios, fluid flow can be quite complex. The calculation of static pressure in more complex situations often requires computational fluid dynamics (CFD) simulations or experimental measurements.
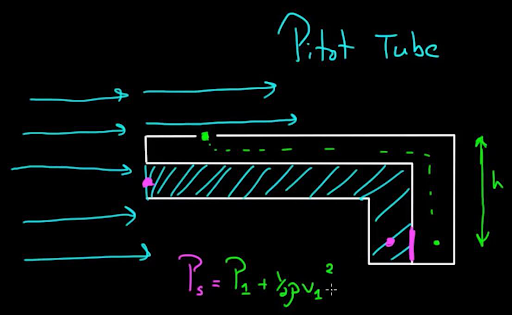
Fig 3. Static pressure
Common examples of using static pressure
Static pressure finds numerous applications in various fields. Here are some common examples of how static pressure is used:
- Barometric Pressure: In meteorology, static pressure is used to measure barometric pressure, which represents the pressure of the Earth's atmosphere at a specific location and time. This is important for weather forecasting and studying atmospheric conditions.
- HVAC Systems: In heating, ventilation, and air conditioning (HVAC) systems, static pressure is used to design and optimize the airflow within ducts and air handling units. It ensures that the air circulates efficiently through the ventilation system, maintaining the desired comfort levels.
- Aircraft and Aerodynamics: In aeronautics, static pressure is used in conjunction with total pressure to calculate airspeed and altitude. It is also essential in designing aircraft wings and bodies to understand lift and drag forces.
- Ventilation Design: In building design, static pressure is used to design ventilation systems, ensuring that fresh air is delivered to occupied spaces while stale air is efficiently exhausted.
- Hydraulics: In fluid dynamics, static pressure is essential in the analysis of fluid flow in pipes, pumps, and hydraulic systems, enabling engineers to determine pressure drops and system performance.
- Water Depth Measurement: In hydrology and oceanography, static pressure is used to measure water depth by utilizing pressure sensors at various depths in water bodies.
- Pressure Measurements: In engineering and research, static pressure is commonly measured using pressure gauges or sensors to monitor the pressure in various systems and processes, ensuring safe and efficient operations.
- Blood Pressure Monitoring: In medicine, static pressure is used to measure blood pressure, which is an important indicator of cardiovascular health.
- Wind Tunnel Testing: In aerodynamics research, wind tunnels use static pressure measurements to study the behavior of airflows around models and prototypes.
- Fuel and Fluid Storage: In industries where fluids like oil, gas, or chemicals are stored, static pressure is monitored to ensure the integrity and safety of the storage containers.
These examples illustrate the broad range of applications for static pressure across multiple fields, emphasizing its significance in engineering, meteorology, aviation, HVAC, and other industries where fluid dynamics and pressure play crucial roles.
dynamic pressure
Dynamic pressure is a term used in fluid dynamics to describe the kinetic energy per unit volume of a moving fluid. It represents the pressure that is associated with the motion of the fluid. Dynamic pressure is a critical parameter in understanding the impact of fluid motion on objects and surfaces in the flow field.
When a fluid (liquid or gas) is in motion, its molecules possess kinetic energy due to their velocity. This kinetic energy results in pressure on the surfaces in contact with the fluid. Unlike static pressure, which is the same in all directions and exists even in a fluid at rest, dynamic pressure is a result of the fluid's velocity and is directional.
The formula to calculate dynamic pressure is
q= ½ ρ. v^2
where:
q = Dynamic pressure (in pascals or any other pressure unit)
ρ = Density of the fluid (in kg/m³ or any appropriate unit)
v = Velocity of the fluid (in m/s or any appropriate unit)
As seen from the formula, the dynamic pressure is directly proportional to the square of the fluid velocity and the fluid density. This means that an increase in fluid velocity or density results in a higher dynamic pressure.
Dynamic pressure is particularly important in aerodynamics, as it helps determine the forces acting on an object (such as an aircraft wing) when it moves through a fluid (air). For instance, in aerodynamics, lift and drag forces are related to the dynamic pressure on the surfaces of the wing. Similarly, in hydrodynamics, dynamic pressure plays a significant role in determining forces on underwater structures or ships as they move through the water.
In summary, dynamic pressure represents the pressure exerted by a moving fluid due to its velocity and is an essential concept in fluid mechanics to understand the impact of fluid motion on objects and surfaces.
Some common examples of using dynamic pressure
Dynamic pressure is a fundamental concept in fluid mechanics and finds numerous practical applications across various fields. Here are some common examples of how dynamic pressure is used:
- Aerodynamics: In aerodynamics, dynamic pressure is crucial for understanding the behavior of airflows around objects like aircraft wings, helicopter blades, and car bodies. It is used to calculate lift and drag forces, which are vital for designing efficient and safe vehicles.
- Wind Energy: Dynamic pressure is employed in the design and analysis of wind turbines. By understanding the dynamic pressure of the wind, engineers can optimize the efficiency and performance of wind energy systems.
- Weather Forecasting: In meteorology, dynamic pressure plays a role in understanding atmospheric conditions and weather patterns. It helps meteorologists predict weather changes and analyze air masses and weather systems.
- Ballistics: In ballistics, dynamic pressure is critical for understanding the aerodynamics of projectiles, such as bullets, rockets, and missiles. It helps in determining trajectory and range.
- Fluid Flow in Pipes: In fluid dynamics, dynamic pressure is used to analyze and design fluid transportation systems, including pipelines and ducts. It is essential for calculating pressure drops and flow rates.
- Water Jet Cutting: In industrial applications, water jet cutting uses high-pressure water jets to cut through materials. Dynamic pressure is a significant factor in achieving the cutting force required.
- Propulsion Systems: In the design of propulsion systems, such as jet engines and rockets, dynamic pressure is crucial for optimizing thrust and overall performance.
- Hydraulics: In hydraulic engineering, dynamic pressure is used to study fluid flow in channels, rivers, and other water systems. It helps in the design of dams, weirs, and flood control structures.
- Fluid Transport in Biological Systems: Dynamic pressure is relevant in studying blood flow in the circulatory system and airflow in the respiratory system.
- Water Sports and Recreation: In sports like surfing and hydrodynamics-based activities, dynamic pressure affects the movement of watercraft and athletes.
These examples illustrate the versatility and importance of dynamic pressure in various fields, ranging from aerospace engineering to meteorology, from industrial applications to biological systems. Dynamic pressure is a fundamental parameter in fluid mechanics, enabling engineers and scientists to understand and optimize fluid flow and its effects on objects and systems.
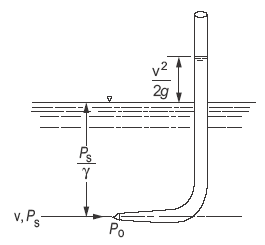
Fig 4. Stagnation pressure
Static vs dynamic pressure
Static pressure and dynamic pressure are two fundamental concepts in fluid mechanics that represent different aspects of pressure in a fluid flow. Here are the key differences between static and dynamic pressure:
Definition
Static Pressure: Static pressure is the pressure exerted by a fluid at rest or moving at a constant velocity in a particular direction. It is isotropic and the same in all directions within the fluid.
Dynamic Pressure: Dynamic pressure, on the other hand, is the pressure associated with the kinetic energy of a moving fluid. It arises due to the fluid's velocity and is directional.
Origin
Static Pressure: Static pressure results from the weight and molecular collisions of the fluid. In a static fluid, the pressure at any point is due to the fluid's weight above that point.
Dynamic Pressure: Dynamic pressure arises due to the motion of the fluid. It represents the pressure that is generated as a fluid flows and its molecules possess kinetic energy.
Measurement
Static Pressure: Static pressure can be measured using pressure gauges or sensors at rest relative to the fluid flow.
Dynamic Pressure: Dynamic pressure is typically calculated based on the fluid's velocity and density using the formula q= ½ ρ. v^2
where
q is the dynamic pressure,
ρ is the fluid density, and
v is the fluid velocity.
Magnitude
- Static Pressure: Static pressure is constant at a specific point in a fluid flow (assuming no changes in elevation).
- Dynamic Pressure: Dynamic pressure varies with the square of the fluid velocity. As the velocity increases, the dynamic pressure increases more rapidly.
Application
- Static Pressure: Static pressure is critical in various applications such as aerodynamics (e.g., lift and drag calculations), HVAC system design, and fluid flow analysis in pipes.
- Dynamic Pressure: Dynamic pressure is crucial in aerodynamics (e.g., airspeed calculations), wind energy systems, and rocket propulsion, where the impact of fluid velocity is significant.
In summary, static pressure is associated with the fluid at rest or moving at a constant velocity, while dynamic pressure represents the pressure resulting from the fluid's motion. Both static and dynamic pressures are important in understanding fluid behavior and have practical applications in various engineering and scientific fields.
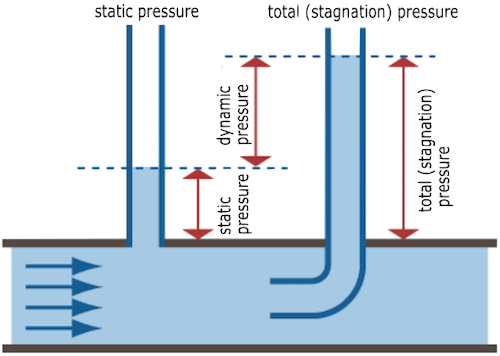
Fig 5. Different pressure scales
Comparing table
Sure, let's create a comparison table to highlight the differences between static pressure and dynamic pressure:
| Aspect | Static Pressure | Dynamic Pressure |
| Definition | Pressure at rest or constant velocity | The pressure associated with fluid motion |
| Origin | Result of fluid weight and molecular collisions | Arises due to fluid velocity and kinetic energy |
| Measurement | Measured with pressure gauges or sensors | Calculated based on fluid velocity and density |
| Magnitude | Constant at a specific point | Varies with the square of fluid velocity |
| Directionality | Isotropic (same in all directions) | Directional, aligned with fluid flow direction |
| Applications | Aerodynamics (e.g., lift and drag calculations), HVAC systems, fluid flow analysis | Aerodynamics (e.g., airspeed calculations), wind energy systems, rocket propulsion |
| Symbol/Notation | P |
q |
| Formula | - | q= ½ ρ. v^2 |
| Units | Pressure units (Pa, psi, atm, etc.) | Pressure units (Pa, psi, atm, etc.) |
Please note that the table highlights the main differences between static and dynamic pressure, but in real-world applications, these pressures are often used together and can change continuously along a fluid flow path. The combination of static and dynamic pressures gives rise to the concept of stagnation pressure, which represents the total pressure when the fluid comes to a stop in the flow field.
Compare static, dynamic, and stagnation pressure
Let's compare static, dynamic, and stagnation pressure in different aspects:
| Aspect | Static Pressure | Dynamic Pressure | Stagnation Pressure |
| Definition | Pressure at rest or moving at a constant velocity | The pressure associated with fluid motion | Total pressure when fluid comes to rest |
| Origin | Results from fluid weight and molecular collisions | Arises due to fluid velocity and kinetic energy | Combine static and dynamic pressures |
| Measurement | Measured with pressure gauges or sensors | Calculated based on fluid velocity and density | Measured with a Pitot tube or similar device |
| Directionality | Isotropic (same in all directions) | Directional, aligned with fluid flow direction | N/A |
| Magnitude | Constant at a specific point | Varies with the square of fluid velocity | Higher than static pressure due to motion |
| Formula | N/A | q= ½ ρ. v^2 | P0= P + q |
| Units | Pressure units (Pa, psi, atm, etc.) | Pressure units (Pa, psi, atm, etc.) | Pressure units (Pa, psi, atm, etc.) |
| Application | Aerodynamics, HVAC systems, fluid flow analysis | Aerodynamics, wind energy, rocket propulsion | Aerodynamics, airspeed calculations, wind tunnel testing |
| Representation | Represents the static state of the fluid | Represents the kinetic energy of the fluid | Represents the total impact of fluid motion |
| Role in Fluid Flow | Influences pressure distribution in fluid systems | Influences fluid forces and velocities | Critical for understanding fluid behavior |
In summary, static pressure represents the pressure at rest or constant velocity, dynamic pressure represents the pressure due to fluid motion and kinetic energy, while stagnation pressure combines static and dynamic pressures to provide the total pressure when the fluid comes to rest. Each type of pressure has specific applications and plays a significant role in fluid dynamics, aerodynamics, and various engineering applications.
Conclusion
In conclusion, static pressure, dynamic pressure, and stagnation pressure are fundamental concepts in fluid mechanics that help us understand the behavior of fluids in motion and at rest. Each type of pressure serves a specific purpose and finds application in various fields, including aerodynamics, HVAC systems, rocket propulsion, and atmospheric studies.
Static pressure represents the pressure of a fluid when it is at rest or moving at a constant velocity. It is isotropic and does not depend on the fluid's motion. Static pressure plays a crucial role in determining pressure distributions in fluid systems and is essential for understanding fluid behavior in various engineering applications.
Dynamic pressure is the pressure associated with the kinetic energy of a moving fluid. It arises due to the fluid's motion and is directional, aligned with the fluid flow direction. Dynamic pressure varies with the square of the fluid velocity, making it a significant factor in aerodynamics, wind energy systems, and rocket propulsion, where the impact of fluid motion is significant.
Stagnation pressure is the total pressure of a fluid when it comes to rest in a flow field. It combines both static pressure and dynamic pressure to represent the maximum impact of fluid motion. Stagnation pressure is measured using a Pitot tube or similar device and plays a critical role in aerodynamics, airspeed calculations, and wind tunnel testing.
In summary, understanding the differences and applications of static, dynamic, and stagnation pressure is vital for engineers, scientists, and researchers working with fluid systems. By using these pressure concepts appropriately, we can better analyze and design various systems, optimize performance, and ensure safe and efficient operations.
To recap
What is stagnation pressure?
Stagnation pressure, also known as total pressure or pitot pressure, is the pressure of a fluid when it comes to a stop, or stagnates, in a flow field. It represents the sum of the static pressure and dynamic pressure of the fluid at a specific point in the flow.
What is static pressure?
Static pressure is the pressure exerted by a fluid at rest or moving at a constant velocity in a particular direction. It is the pressure measured by a pressure gauge at rest relative to the fluid flow.
What is dynamic pressure?
Dynamic pressure is the pressure associated with the kinetic energy of a moving fluid. It arises due to the fluid's velocity and is directional. Dynamic pressure varies with the square of the fluid velocity.
How is stagnation pressure measured?
Stagnation pressure is commonly measured using a device called a Pitot tube. The Pitot tube has a small opening to capture the dynamic pressure and a larger opening perpendicular to the flow to measure the static pressure. The sum of the two gives the stagnation pressure.
What is the difference between static and dynamic pressure?
The main difference lies in their origins and behavior. Static pressure is due to the weight and molecular collisions of the fluid at rest, while dynamic pressure is a result of the fluid's motion and kinetic energy.
What are the units of measurement for stagnation, static, and dynamic pressure?
Stagnation pressure, static pressure, and dynamic pressure are all measured in pressure units such as pascals (Pa), pounds per square inch (psi), or atmospheres (atm).
How is stagnation, static, and dynamic pressure related?
Stagnation pressure is the sum of static pressure and dynamic pressure: P0= P+q It represents the total pressure of the fluid when it comes to rest in the flow field.
What are some applications of stagnation, static, and dynamic pressure?
Stagnation pressure is used in aerodynamics for measuring fluid velocity, static pressure is important in HVAC system design, and dynamic pressure is crucial in wind energy systems and rocket propulsion.
In which scenarios is stagnation pressure highest?
Stagnation pressure is highest when the fluid is brought to a stop, such as when it impacts an object or when it comes to rest in a stagnation tube.
What happens to static and dynamic pressure in a supersonic flow?
In supersonic flows, the dynamic pressure increases significantly due to the high fluid velocities, while the static pressure decreases as the fluid's kinetic energy dominates.
Can static pressure be zero in a moving fluid?
No, static pressure cannot be zero in a moving fluid. Even in a fluid in motion, there is some static pressure, which represents the pressure when the fluid is at rest relative to the flow.
What role does stagnation pressure play in fluid flow measurements?
Stagnation pressure is critical for accurate fluid flow measurements, such as determining airspeed in aircraft or assessing flow rates in pipes, as it represents the total impact of fluid motion.
How is dynamic pressure useful in aerodynamics?
Dynamic pressure is used to calculate aerodynamic forces, such as lift and drag, on aircraft wings and other surfaces moving through a fluid. It helps engineers design efficient and safe vehicles.
What is the relationship between stagnation pressure and kinetic energy?
Stagnation pressure is related to the kinetic energy of the fluid. In a flow where there is no energy loss (adiabatic flow), stagnation pressure is equal to the sum of kinetic and potential energy.
Can dynamic pressure exist without static pressure?
No, dynamic pressure cannot exist without static pressure. In a fluid at rest, there is only static pressure. Dynamic pressure arises due to fluid motion, which occurs in conjunction with static pressure.
References
https://www.mechnflow.com/post/total-pressure-static-pressure-and-dynamic-pressure
https://pipe-flo.com/static-pressure-stagnation-pressure/
https://www.engineersedge.com/fluid_flow/stagnation_pressure_incompressible_fluid_15909.htm
https://www.mecholic.com/2017/05/difference-between-pitot-tube-prandtl-tube.html
Recent Posts
-
Booster Pump Troubleshooting and Maintenance: How to Fix and Prevent Common Issues
1. Introduction Imagine turning on your faucet only to be greeted with a weak trickle of water when …22nd Apr 2025 -
Energy-Efficient Booster Pumps: Selection and Tips for Maximizing Performance
1. Introduction Imagine never having to deal with fluctuating water pressure, noisy pumps, or skyroc …19th Apr 2025 -
Booster Pumps for Sustainable Water Systems: Irrigation and Rainwater Harvesting Solutions
1. Introduction Water scarcity is no longer a distant threat—it’s a reality affecting millions …16th Apr 2025




